25olpsv
Điểm: 100
Alice đang thiết kế những viên gạch đơn giản. Đầu tiên, cô vẽ một hình vuông kích thước ~n \times n~ cm, với ~n~ là một số nguyên dương. Sau đó cô vẽ hai đường tròn bán kính ~n~ cm với tâm lần lượt là góc trái dưới và góc phải trên của hình vuông. Cô thu được một họa tiết hình chiếc lá như hình dưới đây với ~n = 4~.
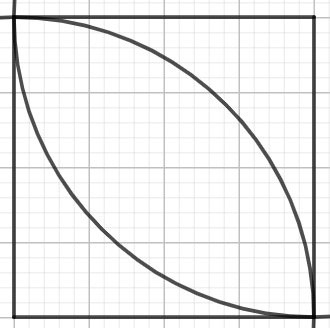
Tiếp theo, Alice tô màu phần "chiếc lá", nghĩa là phần nằm trong hoặc trên biên cả hai đường tròn.
Tuy nhiên, Alice cần biến thiết kế này thành một phiên bản kỹ thuật số. Do đó, cô kẻ các đường thẳng để chia lưới ~n \times n~ cm thành các ô vuông nhỏ kích thước ~1 \times 1~ cm. Sau đó, cô lấy các giao điểm của các đường thẳng, để thu được lưới ~(n + 1) \times (n + 1)~ điểm. Cô đánh dấu những điểm ở vị trí được tô màu trong phiên bản gốc bằng màu đỏ, để thu được hình dưới đây (với ~n = 4~).
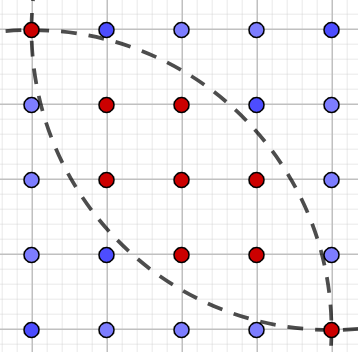
Alice tạo ra một bảng ~(n + 1) \times (n + 1)~ ký tự . hoặc #, với ký tự . ở hàng ~i~ cột ~j~ trong bảng tương ứng với điểm ở hàng ~i~ cột ~j~ trên lưới không được đánh dấu, và ngược lại. Do đó, cô đã tạo ra được bảng ký tự sau với ~n = 4~:
#....
.##..
.###.
..##.
....#
Sau khi đã có thiết kế chiếc lá dạng xuôi, Alice có thể dễ dàng thiết kế chiếc lá dạng ngược, bằng cách thực hiện phép lật theo phương ngang, Với ~n = 4~, đây là bản ký tự cho thiết kế chiếc lá dạng ngược:
....#
..##.
.###.
.##..
#....
Sau khi có phiên bản kỹ thuật số của cả hai kiểu thiết kế, Alice muốn mô phỏng việc sử dụng các viên gạch như thế này để lát một mặt sàn bằng ~a \times b~ viên gạch, được xếp thành một lưới hình chữ nhật gồm ~a~ hàng và ~b~ cột, với ~a, b~ là hai số nguyên dương. Để họa tiết được đẹp mắt, Alice muốn:
- Viên gạch đầu tiên bên trái của hàng trên cùng sử dụng thiết kế chiếc lá dạng xuôi.
- Hai viên gạch có cùng dạng (xuôi, ngược) bất kỳ không được chung cạnh với nhau.
Bảng ký tự dưới đây mô phỏng thiết kế mặt sàn với ~n = 4, a = b = 2~:
#........#
.##....##.
.###..###.
..##..##..
....##....
....##....
..##..##..
.###..###.
.##....##.
#........#
Alice muốn thử mô phỏng với các bộ giá trị ~(n, a, b)~ khác nhau, nhưng cô không có quá nhiều thời gian để vẽ và đánh dấu các viên gạch. Các bạn hãy giúp Alice mô phỏng thiết kế mặt sàn với các bộ giá trị khác nhau nhé.
Dữ liệu - Nhập từ tệp văn bản TILES.inp:
- Một dòng duy nhất gồm ba số nguyên dương ~n, a, b~ ~(1 \le n, a, b \le 1000; a \times n, b \times n \le 1000)~.
Kết quả - Ghi ra tệp văn bản TILES.out:
- Gồm ~(n + 1) \times a~ dòng, mỗi dòng gồm một chuỗi ~(n + 1) \times b~ ký tự
.hoặc#mô phỏng thiết kế mặt sàn sau khi lát gạch.
Chấm điểm
| Điểm | Ràng buộc bổ sung |
|---|---|
| ~32~ | ~n \le 2, a = b = 1~ |
| ~28~ | ~n \le 2~ |
| ~22~ | ~a = b = 1~ |
| ~18~ | Không có ràng buộc gì thêm |
Ví dụ
Dữ liệu (TILES.inp)
4 2 3
Kết quả (TILES.out)
#........##....
.##....##..##..
.###..###..###.
..##..##....##.
....##........#
....##........#
..##..##....##.
.###..###..###.
.##....##..##..
#........##....
Điểm: 100
Hôm nay Nhật Huy muốn mời các em nhỏ trong xóm đến nhà mình chơi. Huy đã đi mời các em nhỏ, và biết được rằng số lượng em nhỏ sẽ đến nhà mình hôm nay sẽ không ít hơn ~l~ và không nhiều hơn ~r~.
Ở nhà Nhật Huy có ~n~ hộp kẹo, hộp kẹo thứ ~i~ có ~a_i~ viên kẹo. Sau khi tất cả các em nhỏ đã đến nhà, Huy sẽ lấy một trong ~n~ hộp kẹo ra và chia đều số kẹo cho các em nhỏ. Huy sẽ cố gắng chọn hộp kẹo sao cho tất cả các em nhỏ đều nhận được số viên kẹo bằng nhau, nhưng có những trường hợp mà Huy không thể chọn được hộp kẹo nào thỏa mãn.
Bạn hãy đếm giúp Huy số giá trị ~x~ với ~l \le x \le r~ sao cho nếu có ~x~ em nhỏ đến chơi nhà thì Huy không thể chọn được hộp kẹo nào thỏa mãn.
Dữ liệu - Nhập từ tệp văn bản NOTDIV.inp:
- Dòng đầu tiên gồm ba số nguyên dương ~n, l, r~ ~(1 \le n \le 10^4, 1 \le l \le r \le 10^6)~.
- Dòng tiếp theo gồm ~n~ số nguyên dương ~a_1, a_2, ..., a_n~ ~(1 \le a_i \le 10^6)~.
Kết quả - Ghi ra tệp văn bản NOTDIV.out:
- Một dòng duy nhất gồm số cách chia kẹo thỏa mãn.
Chấm điểm
| Điểm | Ràng buộc bổ sung |
|---|---|
| ~72~ | ~n \le 50~ |
| ~28~ | Không có ràng buộc gì thêm |
Ví dụ
Dữ liệu (NOTDIV.inp)
4 2 7
7 8 9 10
Kết quả (NOTDIV.out)
1
Giải thích
- Nếu có ~2~ hoặc ~4~ em nhỏ đến nhà, Huy có thể chọn hộp kẹo thứ ~2~.
- Nếu có ~3~ em nhỏ đến nhà, Huy có thể chọn hộp kẹo thứ ~3~.
- Nếu có ~5~ em nhỏ đến nhà, Huy có thể chọn hộp kẹo thứ ~4~.
- Nếu có ~7~ em nhỏ đến nhà, Huy có thể chọn hộp kẹo thứ ~1~.
- Trường hợp duy nhất mà Huy không thể chọn hộp kẹo nào thỏa mãn là khi có ~6~ em nhỏ đến nhà.
Điểm: 100
Nhật Huy có ~n~ cái kẹo và muốn chia hết số kẹo này cho ba bạn Mayly, Peace và Sunny. Biết rằng:
- Mayly không muốn số lượng kẹo mình được nhận là một số chia hết cho ~2~.
- Peace không muốn số lượng kẹo mình được nhận là một số chia hết cho ~3~.
- Sunny không muốn số lượng kẹo mình được nhận là một số chia hết cho ~4~.
- Tất cả các bạn đều không muốn số lượng kẹo mình được nhận bằng với số lượng kẹo mà người khác được nhận.
Huy muốn nhờ bạn tính xem Huy có bao nhiêu cách chia kẹo thỏa mãn. Các bạn hãy tính giúp Huy nhé.
Dữ liệu - Nhập từ tệp văn bản CANDY.inp:
- Một dòng duy nhất gồm một số nguyên dương ~n~ - số kẹo mà Huy có ~(1 \le n \le 10^6)~.
Kết quả - Ghi ra tệp văn bản CANDY.out:
- Một dòng duy nhất gồm số cách chia kẹo thỏa mãn.
Chấm điểm
| Điểm | Ràng buộc bổ sung |
|---|---|
| ~42~ | ~n \le 200~ |
| ~36~ | ~n \le 5000~ |
| ~22~ | Không có ràng buộc gì thêm |
Ví dụ
Dữ liệu (CANDY.inp)
6
Kết quả (CANDY.out)
3
Giải thích
Có ~3~ cách chia thỏa mãn như sau:
- Cách 1: Mayly nhận được ~1~ cái kẹo, Peace nhận được ~2~ cái kẹo, Sunny nhận được ~3~ cái kẹo.
- Cách 2: Mayly nhận được ~3~ cái kẹo, Peace nhận được ~1~ cái kẹo, Sunny nhận được ~2~ cái kẹo.
- Cách 3: Mayly nhận được ~3~ cái kẹo, Peace nhận được ~2~ cái kẹo, Sunny nhận được ~1~ cái kẹo.
Điểm: 100
Trong văn hóa Á Đông xưa, các con số ~1, 5, 9~ thường được xem là tốt lành, vì chúng ứng với sinh, tức sinh sôi, nảy nở, trong chu trình sinh - lão - bệnh - tử.
Huy đang nghiên cứu các văn bản cổ, và anh thấy người xưa gọi một số là cát tường nếu biểu diễn thập phân của nó chỉ bao gồm các chữ số ~1, 5~ hoặc ~9~, và không có hai chữ số liên tiếp nào giống nhau. Như vậy, các số cát tường đầu tiên là ~1, 5, 9, 15, 19, 51, 59, 91, 95, 151, ...~.
Huy tiếp tục nghiên cứu, và anh thấy người xưa đã cố gắng tách các số tự nhiên thành tổng của hai số cát tường theo những cách khác nhau. Ví dụ, số ~2~ có thể được tách thành ~1 + 1~, ~10~ có thể được tách thành ~5 + 5~ hoặc ~1 + 9~. Họ ký hiệu ~f_x~ là số cách tách tổng của hai số cát tường. Như vậy, ~f_2 = 1~ và ~f_{10} = 2~. Huy tìm thấy một bài toán, trong đó yêu cầu tính tổng ~S = f_l + f_{l + 1} + ... + f_r~, nhưng vẫn chưa có lời giải hay công thức cụ thể. Bạn hãy giúp Huy tính toán giá trị ~S~ với các cặp ~l, r~ khác nhau để có thể giúp Huy tìm ra công thức tổng quát cho bài toán nhé.
Dữ liệu - Nhập từ tệp văn bản INTEGER.inp:
- Một dòng duy nhất gồm hai số nguyên dương ~l, r~ ~(1 \le l \le r \le 10^{18})~.
Kết quả - Ghi ra tệp văn bản INTEGER.out:
- Một dòng duy nhất gồm giá trị ~S~ tìm được.
Chấm điểm
| Điểm | Ràng buộc bổ sung |
|---|---|
| ~44~ | ~r \le 2000~ |
| ~34~ | ~r \le 2 \times 10^5~ |
| ~22~ | Không có ràng buộc gì thêm |
Ví dụ
Dữ liệu (INTEGER.inp)
2 10
Kết quả (INTEGER.out)
4
Giải thích
Ta có ~f_2 = 1, f_6 = 1~ và ~f_{10} = 2~. Có thể thấy các giá trị còn lại không có cách nào để tách thành hai số cát tường.
Điểm: 100
Huy có một dãy số gồm ~2n~ phần tử ~a_1, a_2, ..., a_{2n}~, trong đó mỗi số nguyên dương không lớn hơn ~n~ xuất hiện đúng hai lần. Huy định nghĩa khoảng cách của một vị trí ~i~ trong dãy số và một cặp phần tử cùng có giá trị ~j~ là ~D(i, j)~, được tính theo công thức:
$$D(i, j) = (|x_j - i| + 1) \times (|y_j - i| + 1)$$
trong đó ~x_j, y_j~ là hai vị trí của hai phần tử có giá trị ~j~.
Huy muốn tính xem với mỗi vị trí ~i~ thì khoảng cách gần nhất giữa ~i~ và một cặp phần tử bất kỳ là bao nhiêu, hay nói cách khác Huy muốn tìm giá trị ~D(i, j)~ nhỏ nhất với mọi ~j~. Tuy nhiên do số vị trí quá lớn nên Huy không thể tính nhanh được, các bạn hãy giúp Huy nhé.
Dữ liệu - Nhập từ tệp văn bản PAIR.inp:
- Dòng đầu tiên gồm một số nguyên dương ~n~ ~(1 \le n \le 10^5)~.
- Dòng tiếp theo gồm ~2n~ số nguyên dương ~a_1, a_2, ..., a_{2n}~ ~(1 \le a_i \le n)~.
- Dữ liệu đầu vào đảm bảo trong dãy ~a~ có đúng hai phần tử có giá trị ~i~ với mỗi ~i~ thỏa mãn ~1 \le i \le n~.
Kết quả - Ghi ra tệp văn bản PAIR.out:
- Một dòng duy nhất gồm ~2n~ số nguyên dương, số nguyên dương thứ ~i~ là khoảng cách ngắn nhất của một cặp số bất kỳ với vị trí ~i~.
Chấm điểm
| Điểm | Ràng buộc bổ sung |
|---|---|
| ~23~ | ~a_{2i - 1} = a_{2i}~ với mọi ~i~ |
| ~33~ | ~n \le 2000~ |
| ~44~ | Không có ràng buộc gì thêm |
Ví dụ
Dữ liệu (PAIR.inp)
2
1 2 2 1
Kết quả (PAIR.out)
4 2 2 4
Giải thích
- Cặp phần tử có giá trị ~1~ xuất hiện tại hai vị trí ~1~ và ~4~.
- Khoảng cách giữa vị trí ~1~ và cặp phần tử có giá trị ~1~ là: $$D(1, 1) = (|x_1 - 1| + 1) \times (|y_1 - 1| + 1) = (|1 - 1| + 1) \times (|4 - 1| + 1) = 4$$
- Cặp phần tử gần nhất với vị trí ~1~ và vị trí ~4~ là cặp phần tử có giá trị ~1~, với khoảng cách là ~4~.
- Cặp phần tử gần nhất với vị trí ~2~ và vị trí ~3~ là cặp phần tử có giá trị ~2~, với khoảng cách là ~2~.
Điểm: 100
Câu lạc bộ SQRT dự định tổ chức các đợt trại hè Tin học dành cho học sinh. Câu lạc bộ muốn mời hai thí sinh IOI, LKT và ĐHH, đến giao lưu với các trại sinh. Tuy nhiên, lịch trình của hai vị khách mời này rất bận rộn nên họ chỉ có thể đến giao lưu với các trại sinh trong một số ngày nhất định, cụ thể:
- LKT chỉ có thể đến được vào những ngày là bội của ~a~, nghĩa là các ngày ~a, 2a, 3a, ...~.
- ĐHH chỉ có thể đến được vào những ngày là bội của ~b~, nghĩa là các ngày ~b, 2b, 3b, ...~.
biết rằng hôm nay là ngày ~1~.
Câu lạc bộ SQRT muốn tổ chức trại hè trong ~d~ ngày, bắt đầu từ ngày thứ ~k~. Hay nói cách khác, trại hè sẽ diễn ra trong các ngày ~k, k + 1, k + 2, ..., k + d - 1~. Câu lạc bộ muốn trong ~d~ ngày này, phải có ít nhất một ngày LKT có thể đến giao lưu, và ít nhất một ngày ĐHH có thể đến giao lưu. Lưu ý rằng hai ngày này có thể trùng nhau. Các bạn hãy giúp câu lạc bộ SQRT tìm ra thời điểm sớm nhất mà câu lạc bộ SQRT có thể bắt đầu trại hè, hay nói cách khác, tìm ra giá trị ~k~ nhỏ nhất.
Dữ liệu:
- Dòng đầu tiên gồm một số nguyên dương ~T~ là số bộ dữ liệu ~(1 \le T \le 100)~.
- ~T~ dòng tiếp theo, mỗi dòng gồm ba số nguyên dương ~a, b, d~ ~(1 \le a, b, d \le 3 \times 10^9)~.
Kết quả:
- Với mỗi bộ dữ liệu, in ra kết quả trên một dòng.
Chấm điểm
| Điểm | Ràng buộc bổ sung |
|---|---|
| ~6~ | ~d = 1~ |
| ~13~ | ~a, b \le 200~ |
| ~15~ | ~a, b \le 2 \times 10^4~ |
| ~27~ | ~d \le 2~ |
| ~39~ | Không có ràng buộc gì thêm |
Ví dụ
Dữ liệu
2
5 7 3
5 7 2
Kết quả
5
14
Giải thích
- Ở bộ dữ liệu đầu tiên, trại hè diễn ra vào các ngày ~5, 6, 7~. LKT có thể đến giao lưu vào ngày ~5~, trong khi ĐHH có thể đến giao lưu vào ngày ~7~.
- Ở bộ dữ liệu thứ hai, trại hè diễn ra vào các ngày ~14, 15~. LKT có thể đến giao lưu vào ngày ~15~, trong khi ĐHH có thể đến giao lưu vào ngày ~14~.