Một cuộc thi lập trình điều khiển robot được ban tổ chức olympic 30-4 thiết kế cho các bạn yêu thích Tin học. Bạn tổ chức thiết kế một sơ đồ cho robot di chuyển gồm n địa điểm được đánh số từ 1 tới n và được nối với nhau bởi m đường hai chiều, đánh số từ 1 tới m. Con đường thứ i nối hai địa điểm ~u_i, v_i~ với trọng số ~w_i~ ~(1 \leq u_i, v_i \leq n; 1 \leq w_i \leq 10^9)~. Tại mỗi địa điểm ghi một số nguyên ~a_i~ là số điểm thường mà robot nhận được khi đến địa điểm này lần đầu.

Ban tổ chức chọn một địa điểm s làm địa điểm xuất phát và robot nhận được điểm thường đầu tiên tại địa điểm này. Mỗi khi đi qua con đường có trọng số k sẽ bị phát thẻ phạt. Robot được phép bị phát không quá k thẻ phạt. Khi bị phát thẻ, robot sẽ không được phép nhận thêm điểm thường ở bất kỳ địa điểm nào nữa.

Yêu cầu: Hãy xác định số địa điểm lớn nhất mà robot có thể đi qua.

Dữ liệu: vào từ file văn bản ROBOT.INP

• Dòng đầu tiên chứa 4 số nguyên ~n, m, s, v~ và ~k~ ~(1 \leq n \leq 10^5; 1 \leq m \leq 2 \cdot 10^5)~.
• Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ ~(1 \leq a_i \leq 10^9)~.
• Dòng thứ i trong m dòng tiếp theo chứa 3 số nguyên ~u_i, v_i, w_i~ ~(1 \leq u_i, v_i \leq n; 1 \leq w_i \leq 10^9)~.

Kết quả: ghi ra file văn bản ROBOT.OUT một số nguyên duy nhất là số địa điểm tối đa mà robot có thể đi qua.

Ví dụ:

Input

6 7 3 1
3 4 2 3 2 7
1 6 10
1 5 8
5 2 12
2 6 10
2 3 5
3 4 1
3 5 11

Output

5

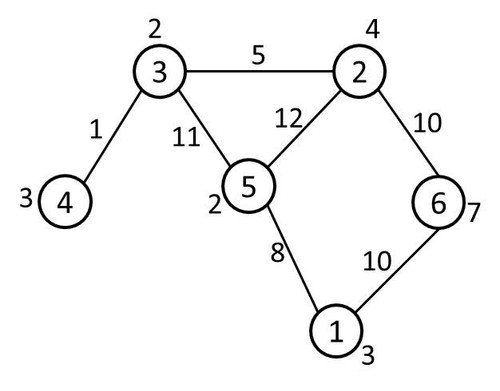
Minh hoạ

Giải thích: Robot đi ~3 \to 4 \to 3 \to 2 \to 5 \to 1~. Robot đi ~3 \to 4 \to 3 \to 2~ nhận được điểm thường là 9. Đi từ 2 sang 5 bị nhận 1 thẻ phạt và từ đó không được nhận thêm điểm thường.

Ràng buộc:

• ~30\%~ số điểm có ~n = m - 1 < 10^3; u_i = i, v_i = i + 1; k = 0~.
• ~20\%~ số điểm có ~k = 0; n \leq 10^3~.
• ~20\%~ số điểm có ~k = 0; n \leq 10^5~.
• ~30\%~ số test có ~k = 1~.